FBISE Physics Short Questions
FBISE Physics Short Questions
FBISE Physics Short Questions for Class 9
BISE Physics MCQs for Class 9 of Unit 1 Physical Quantities and Measurements
1.2 What is the difference between base quantities and derived quantities? Give three examples in each case.
Ans:
Sr.# | Base Quantities | Derived Quantities |
| Base quantities are the
| The quantities that are expressed in terms of base quantities are called derived quantities. |
| Base quantities are seven (07) in numbers. | Derived quantities are more than seven (07) in numbers. |
| For Example: length, mass, time | For Example: area, volume, speed |
1.3 Pick out the base units in the following:
joule, newton, kilogramme, hertz, mole, ampere, metre, kelvin, coulomb and watt.
Ans:
Base Units: kilogramme, mole, ampere, meter, kelvin
1.4 Find the base quantities involved in each of the following derived quantities:
(a) speed (b) volume (c) force (d) work
1.5 Estimate your age in seconds.
1.6 What role SI units have played in the development of science?
Ans:
i. With the developments in the field of science and technology, the need of commonly acceptable system of units was seriously felt all over the world particularly to exchange scientific and technical information. The SI system fulfils this need.
ii. SI unit is in use all over the world.
iii. They are easy to use because multiples and sub multiples of different units are obtained simply by multiplying or dividing with 10 or some power of 10.
1.7 What is meant by vernier constant?
Ans:
The smallest reading that can be measured by a vernier calliper is called the vernier constant or least count of vernier callipers. Its value is 0.1 mm or 0.01 cm.
OR
It is difference between one small division on main scale and one vernier scale division.
Vernier Constant = (One small division on main scale) – (One vernier scale division)
= 1 mm – 0.9 mm
= 0.1 mm
1.8 What do you understand by the zero error of a measuring instrument?
Ans:
Zero error is basically a systematic error which exist in measuring instrument. It is a type of error in which an instrument gives a reading when the true reading at that time is zero.
For Example: In vernier callipers, when no object is placed between the jaws of vernier callipers, close the jaws of vernier callipers gently, if the zero of main scale does not coincide with the zero of vernier scale then error is called zero error.
1.9 Why is the use of zero error necessary in a measuring instrument?
Ans:
The use of zero error is very necessary in the measuring instruments, if zero error exists in an instrument it shows measurement more or less than actual measurement. i.e. incorrect measurement. The measurement can be corrected by zero correction.
1.10 What is a stopwatch? What is the least count of a mechanical stopwatch you have used in the laboratories?
Ans:
A stopwatch is used to measure the time interval of an event. The mechanical stopwatch that we used in laboratories has a least count of 0.1 second.
1.11 Why do we need to measure extremely small interval of times?
Ans: We need to measure extremely small intervals of times
i. To calculate instantaneous time rate of change of a variable.
ii. For greater accuracy in results.
iii. In physics many events occur for very short interval of time, to study that events.
1.12 What is meant by significant figures of a measurement?
Ans:
“In any measurement all the accurately known digits and the first doubtful digit in are called significant figures.”
For example, a student measures the length of a book as 18 cm using a measuring tape. The numbers of significant figures in his/her measured value are two. The left digit 1 is the accurately known digit. While the digit 8 is the doubtful digit for which the student may not be sure.
1.13 How is precision related to the significant figures in a measured quantity?
Ans:
Significant figures reflect the precision of a measured value of a physical quantity. More significant figure means greater precision.
FBISE Physics MCQs for Class 9 of Unit 2 Kinematics
2.2 Explain translatory motion and give examples of various types of translatory motion?
Translatory Motion
“In translational motion, a body moves along a line without any rotation. The line may be straight or curved”
Translatory motions can be divided into three types as given below
i. Linear Motion,
ii. Circular Motion
iii. Random Motion
i. Linear Motion
“Straight line motion of a body is known as its linear motion.”
For Example:
· a car moving on a straight and level road is linear motion.
· Aeroplanes flying straight in air.
· objects falling vertically down
ii. Circular Motion
“The motion of an object in a circular path is known as circular motion”
For Example:
· A car moving along a circular track possesses circular motion
· Motion of the Earth around the Sun
· Motion of the moon around the Earth.
iii. Random Motion
“The disordered or irregular motion of an object is called random motion.”
For Example:
· Motion of insects and birds is random motion
· The motion of dust or smoke particles in the air is also random motion.
· The Brownian motion of a gas or liquid molecules along a zig-zag
path is also an example of random motion.
2.3 Differentiate between the following:
i. Rest and motion.
ii. Circular motion and rotatory motion.
iii. Distance and displacement
iv. Speed and velocity.
v. Linear and random motion.
vi. Scalars and vectors.
i. Rest and motion
Rest:
A body is said to be at rest if it does not change its position with respect to its surroundings.
Motion:
A body is said to be in motion if it changes its position with respect to its surroundings.
ii. Circular motion and rotatory motion.
Sr. No. | Circular Motion | Rotatory Motion |
1 | The motion of an object in a circular path is known as circular motion. For Example: · A car moving along a circular track possesses circular motion · Motion of the Earth around the Sun · Motion of the moon around the Earth. | The spinning motion of a body about its axis is called its rotatory motion. For Example: · The motion of a wheel about its axis. · The motion of the Earth about its · The motion of a top |
2 | In circular motion, the point about | In rotatory motion, the line (axis), around which a body moves about, is passing through the body itself. |
3 |
|
|
iii. Distance and displacement
Sr. No. | Distance | Displacement |
1 | Length of a path between two points is called the distance between those points. | Displacement is the shortest distance between two points which has magnitude and direction. |
2 | Distance is a scalar quantity, | Displacement is a vector quantity. |
3 | It is denoted by S. | It is denoted by d. |
iv. Speed and velocity
Sr. No. | Speed | Velocity |
1 | The distance covered by an object in unit time is called its speed. Speed = Distance covered/Time Taken | The rate of displacement of a body is called its velocity Speed = Displacement/Time Taken. |
2 | Speed is a scalar quantity, | Velocity is a vector quantity. |
3 | It is denoted by v. | It is denoted by v. |
v. Linear and random motion.
Linear Motion
“Straight line motion of a body is known as its linear motion.”
For Example:
· a car moving on a straight and level road is linear motion.
· Aero planes flying straight in air.
· objects falling vertically down
Random Motion
“The disordered or irregular motion of an object is called random motion.”
For Example:
· Motion of insects and birds is random motion
· The motion of dust or smoke particles in the air is also random motion.
· The Brownian motion of a gas or liquid molecules along a zig-zag
path is also an example of random motion.
vi. Scalars and vectors.
Scalars
A physical quantity which can be completely described by its magnitude is called a scalar.
Examples: mass, length, time, speed, volume, work and energy.
Vectors
A vector quantity is described completely by magnitude and direction.
Examples: velocity, displacement, force, momentum, torque, etc.
2.4 Define the terms speed, velocity, and acceleration.
Speed
“The distance covered by an object in unit time is called its speed.”
\[Speed=\frac{Distance Covered}{Time Taken}\]
\[v=\frac{S}{t}\]
Speed is a scalar quantity. SI unit of speed is metre per second (ms-1).
Velocity
“The rate of displacement of a body is called its velocity”
\[velocity=\frac{Displacement}{Time Taken}\]
\[\overline{v}=\frac{\overline{d}}{t}\]
velocity is a vector quantity. SI unit of speed is metre per second (ms-1).
Acceleration
“Acceleration is defined as the rate of change of velocity of a body.”
\[acceleration=\frac{Change in velocity}{Time Taken}\]
\[acceleration=\frac{final velocity - initial velocity}{Time Taken}\]
\[\overline{a}=\frac{\overline{v_{f}}-\overline{v_{i}}}{t}\]
acceleration is a vector quantity. SI unit of acceleration is metre per second per second (ms-2).
2.5 Can a body moving at a constant speed have acceleration?
Yes, a body moving at constant speed has acceleration if it moves along a circular track because the direction of motion of a body along a circular track is continuously changing.
2.6 How do riders in a Ferris wheel possess translatory motion but not rotatory motion?
Rider in a Ferris wheel possess circular motion because they are moving in a circle of constant radius. As circular motion is a type of translatory motion. Therefore, riders in a Ferris wheel possess translatory motion.
As Rider in a Ferris wheel are not moving about their axis, therefore Rider in a Ferris wheel does not possess rotatory motion.
2.7 Sketch a distance-time graph for a body starting from rest. How will you determine the speed of a body from this graph?
Distance time graph of a body starting at rest is shown in the figure below
\[Speed of the object= Slope of line AB\]
\[Speed of the object=\frac{Distance EF}{Time CD}\]
\[Speed of the object=\frac{20 m}{10 s}\]
\[Speed of the object= 2 ms^{-1}\]
2.8 What would be the shape of a speed -time graph of a body moving with variable speed?
The shape of speed-time graph of a body moving with variable velocity is not a straight line.
2.9 Which of the following can be obtained from speed - time graph of a body?
(i) Initial speed.
(ii) Final speed.
(iii) Distance covered in time t.
(iv) Acceleration of motion.
All of these can be measured by speed-time graph.
2.10 How can vector quantities be represented graphically?
Graphically, a vector can be represented by a line segment with an arrowhead. The length of the line gives the magnitude of the vector on a selected scale. While the direction of the line gives the direction of the vector.
2.11 Why vector quantities cannot be added and subtracted like scalar quantities?
Scalars quantities are added or subtracted by simple arithmetic methods because scalar quantities have no direction. Since vectors have magnitude as well as direction, therefore vectors cannot be added and subtracted by simple arithmetic methods like scalars. Vectors are added by head to tail rule,
2.12 How are vector quantities important to us in our daily life?
Sometimes it would be meaningless to describe some quantities without directions therefore vectors quantities are very important in our daily life.
For Example.
Distance of a place from reference point is insufficient to locate that place. The direction of that place from reference point is also necessary to locate that place.
2.13 Derive equations of motion for uniformly accelerated rectilinear motion.
First (1st) equation of motion
Second (2nd) equation of motion
Third (3rd) equation of motion
2.14 Sketch a velocity - time graph for the motion of the body. From the graph explaining each step, calculate total distance covered by the body..
FBISE Physics MCQs for Class 9 of Unit 3 Dynamics
3.2 Define the following terms:
(i) Inertia (ii) Momentum (iii) Force
(iv) Force of friction (v) Centripetal force
Ans: Inertia
“Inertia of a body is its property due to which it resists any change in its state of rest or motion”
Momentum
“Momentum of a body is the quantity of motion it possesses due to its mass and velocity”
Momentum is a vector quantity. It is represented by P . The momentum P of a body of mass m moving with velocity v is given by the relation
P = mv
SI unit of momentum is kgms-1.
Force
“A force moves or tends to move, stops or tends to stop the motion of a body. The force can also change the direction of motion of a body”
Force of Friction
“The force that opposes the motion of moving objects is called force of friction”
Centripetal
“Centripetal force is a force that keeps a body to move in a circle.”
The Centripetal force is given by the following formula
\[F_{c} = \frac{mv^{2}}{r}\]
3.3 What is the difference between:
(i) Mass and weight
(ii) Action and reaction
(iii) Sliding friction and rolling friction
Ans: Difference between mass and weight
Sr. No. | Mass | Weight |
1. | Mass of a body is the quantity of matter possessed by the body. | Weight of a body is equal to the force with which earth attracts it. |
2. | It is a scalar quantity. | It is a vector quantity. |
3. | Its SI unit is kilogram (kg). | Its SI unit is newton (N). |
4. | Its value does not change with place. | Its value changes from place to place. |
5. | Mass is measured by comparison with standard masses using a beam balance. | Weight is measured with spring balance. |
Difference Between Action and Reaction
Sr. No. | Action | Reaction |
1 | Action is a cause. | Reaction is an effect due to the cause. |
2 | Action is the act that you perform on something expecting something to happen, | Reaction is the happening of something which we are expecting in the result of action. |
3 | Action force acts on one body. | Reaction force acts on another body. |
4 | Action force acts in one direction | Reaction force acts in other direction |
5 | The force exerted on an object is the action, | The force experienced by the object due to action as a consequence of Newton's third law is the reaction. |
Difference Between Sliding and Rolling Friction
Sr. # | Sliding Friction | Rolling Friction |
1 | When an object slides over the surface of another object it is called sliding friction. | When an object rolls over the surface of another object it is called rolling friction. |
2 | Sliding friction takes place due to interlocking between microscopic surfaces. | Rolling friction takes place due to the deformation of surfaces. |
3 | The coefficient of sliding friction depends on the texture of the surface and temperature to a certain extent. | The coefficient of rolling friction is dependent on the radius of the rolling object, the depth to which the object can sink, and the toughness of the surface |
4 | It is greater than rolling friction. | It is lesser than sliding friction. |
5 | Only a point on the surface remains in contact with the object. | A finite area of the surface remains in contact with the object |
6 | Sliding friction is given by the relation Fs = µs N | Rolling friction is given by the relation. Fr = µr N |
3.4 What is the law of Inertia?
Ans: Newtons First law of motion is also known as law of inertia it states that
“A body continues its state of rest or of uniform motion in a straight line provided no net force acts on it.”
3.5 Why is it dangerous to travel on the roof of a bus?
3.6 Why does a passenger move outward when a bus takes a turn?
Ans: When a bus takes a sharp turn, passengers fall in the outward direction. It is due to inertia that they want to continue their motion in a straight line and thus fall outwards.
3.7 How can you relate a force with the change of momentum of a body?
“When a force acts on a body, it produces an acceleration in the body and will be equal to the rate of change of momentum of the body.”
It is given by the relation
\[F = \frac{P_{f}-P_{i}}{t}\]
3.8 What will be the tension in a rope that is pulled from its ends by two opposite forces 100 N each?
Ans: 10 N
Explanation:
3.9 Action and reaction are always equal and opposite. Then how does a body move?
Ans: Action and reaction do not act on the same body. Action is applied on one body due to which an equal and opposite reaction is acting on another body. Both of these do not cancel each other due to which the body will move.
3.10 A horse pulls the cart. If the action and reaction are equal and opposite, then how does the cart move?
Ans: The cart moves due to the reaction force of ground.
Explanation:
The horse apply force on cart and ground, in the reaction cart and ground both apply force on the horse. The force of horse on cart and the force of cart on horse both cancel each other. The horse and cart both move due to the reaction force of ground.
3.11 What is the law of conservation of momentum?
Ans: The law of conservation of momentum states that
“The momentum of an isolated system of two or more than two interacting bodies remains constant.”
3.12 Why is the law of conservation of momentum important?
Ans: By using law of conservation of momentum, it is possible to calculate force, velocity, acceleration of a body. Most of elementary particles are discovered by use of this law.
3.13 When a gun is fired, it recoils. Why?
Ans: The gun recoils to conserve the momentum of the system.
Explanation
Consider the system of gun and a bullet. Before firing the gun both the gun and bullet are at rest, so the total momentum of the system is zero. As the gun is fired bullet moves in the forward direction and gun recoils so that total momentum after firing also become zero.
3.14 Describe two situations in which force of friction is needed.
Ans: Following are the situations in which force of friction is needed
1. We cannot write if there would be no friction between paper and the pencil.
2. Friction enables us to walk on the ground.
3. Birds could not fly, if there is no air resistance. The reaction of pushed air enables the birds to fly.s
3.15 How does oiling the moving parts of a machine lowers friction?
Ans: The oil coats the surfaces of the moving parts and makes them slippery. They slide over each other more easily, so there is less friction. Friction is always parallel to the surface in contact.
3.16 Describe ways to reduce friction.
Ans: Following are the methods of reducing friction
· Making the sliding surfaces smooth.
· Making the fast moving objects a streamline shape (fish shape) such as cars, aero planes, etc. This causes the smooth flow of air and thus minimizes air resistance at high speeds.
· Lubricating the sliding surfaces.
· Using ball bearings or roller bearings. Because the rolling friction is lesser than the sliding friction
3.17 Why rolling friction is less than sliding friction?
Ans: When an object slides over the surface of another object it is called sliding friction. When an object rolls over the surface of another object it is called rolling friction. The force of friction depends on the area of contact between the two surfaces. Greater the area of contact between two surfaces greater is the force of friction. In case of rolling friction, the area of contact between two surfaces is lesser than in case of sliding friction. Therefore, rolling friction is lesser than the sliding friction.
3.18 What you know about the following:
(i) Tension in a string
(ii) Limiting force of friction
(iii) Braking force
(iv) Skidding of vehicles
(v) Seatbelts
(vi) Banking of roads
(vii) Cream separator
Ans:
(i) Tension in a string (Not included in the smart Syllabus)
(ii) Limiting force of friction
Friction is equal to the applied force that tends to move a body at rest. It increases with the applied force. Friction can be increased to certain maximum value. It does not increase beyond this. The maximum value of friction is known as the force of limiting friction (Fs). It is given by the formula
Fs = µR
Here R is the normal reaction and µ is the coefficient of static friction.
(iii) Braking force (Not included in the smart Syllabus)
(iv) Skidding of vehicles (Not included in the smart Syllabus)
(v) Seatbelt (Not included in the smart Syllabus)
(vi) Banking of roads (Not included in the smart Syllabus)
(vii) Cream separator (Not included in the smart Syllabus)
3.19 What would happen if all friction suddenly disappears?
Ans: Following things will happen If all the friction is suddenly disappear
1. We would not be able to walk
2. We would not be able to write with pencil
3. We would not be able to pick objects.
4. We would not be able to run vehicles and brakes of the vehicles would not work.
In short everything would be out of order and whole system on the earth would collapse.
3.20 Why the spinner of a washing machine is made to spin at a very high speed?
(Not included in the smart Syllabus)
FBISE Physics MCQs for Class 9 of Unit 4 Turning Effect of Forces
4.2 Define the following:
(i) resultant vector
(ii) torque
(iii) centre of mass
(iv) center of gravity
Ans: Resultant Vector
“A resultant vector is a single vector that has the same effect as the combined effect of all the vectors to be added.”
Torque
“The turning effect of a force is called torque or moment of the force.”
Torque is denoted by the symbol τ and is given by the relation
τ = F x L
Torque is a vector quantity, and its SI unit is newton-meter (Nm).
Centre of Mass
“Centre of mass of a system is such a point where an applied force causes the system to move without rotation”
Generally, centre of mass of a system is represented by “O”.
Centre of gravity
“A point where the whole weight of the body appears to act vertically downward is called centre of gravity of a body”
Generally, centre of gravity of a body is represented by “G”.
4.3 Differentiate the following:
(i) like and unlike forces
(ii) torque and couple
(iii) stable and neutral equilibrium
Ans:
(i) Like and Unlike Forces
Sr. # | Like Parallel forces | Unlike Parallel Forces |
1 | Like parallel forces are the forces that are parallel to each other and have the same direction. | Unlike parallel forces are the forces that are parallel but have directions opposite to each other |
(ii) Torque and Couple
Sr. # | Torque | Couple |
1. | The turning effect of the force is called torque. | A couple is formed by two unlike parallel forces of same magnitude but not acting along the same line. |
2. | Torque is produced by a single force. | Couple is formed by two forces. |
3. | Torque is the product of force and moment arm L. Torque= Force x Moment arm | Torque Produced by the couple is given by the product of one of the two forces and the perpendicular distance between them. |
4. | Examples i. Unscrewing a nut using a wrench. ii. Open or closing a door by pushing it about its hinges. | Examples i. Turning a steering wheel of a car by applying two hands form a couple. ii. Turning of a tap is based upon the principle of couple. |
5. | In the case of a FREE body (not fixed to a pivot), a torque produces not only rotational motion but also translational motion of the body. | A couple NEVER produces translational motion in a free body. |
(iii) Stable and Neutral Equilibrium
Sr.# | Stable Equilibrium | Neutral Equilibrium |
1 | A body is said to be in stable equilibrium if after a slight tilt it returns to its previous position | If a body remains in its new position when disturbed from its previous position, it is said to be in a state of neutral equilibrium. |
2 | When a body is in stable equilibrium, its centre of gravity is at the lowest position. | In neutral equilibrium, the centre of gravity of the body remains at the same height, irrespective to its new |
3 | A body remains in stable equilibrium as long as the centre of gravity acts through the base of the body | In neutral equilibrium, all the new states in which a body is moved, are the stable states and the body, remains in its new state |
4 | Examples of stable equilibrium · Chair lying on the floor · The heavy base of the vehicle · Table lying on the ground · Cone lying on its base by lowering its centre of gravity · Bottle lying on its base | Examples of neutral equilibrium · Ball moving on the ground · Motion of sphere · A roller · A pencil lying horizontally · An egg lying horizontally on a flat surface |
4.4 How head to tail rule helps to find the resultant of forces?
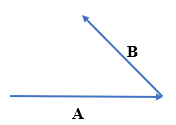
First select a suitable scale. Then draw the vectors of all the forces according to the scale, such as vectors A and B as shown in the figure blow
Take any one of the vectors as first vector e.g., vector A. Then draw next vector B such that its tail coincides with the head of the first vector A. as shown in the figure below.
Similarly, draw the next vector for the third force (if any) with its tail coinciding with the head of the previous vector and so on.
Now draw a vector R such that its tail is at the tail of vector A, the first vector, while its head is at the head of vector B, the last vector as shown in figure below.
Vector R represents the resultant force completely in magnitude and direction.
4.5 How can a force be resolved into its perpendicular components?
Resolution of Forces
Definition
“Splitting up of a force into two mutually perpendicular components is called the resolution of that force”
Method of Resolving a Force into its perpendicular components
Consider a force F represented by line OA making an angle q with x-axis as shown in the figure below
Draw a perpendicular AB on x-axis from A. According to head to tail rule, OA is the resultant of vectors represented by OB and BA. Thus
OA = OB + BA -------- (1)
The components OB and BA are perpendicular to each other. They are called the perpendicular components of OA representing force F.
Here
OB represents x-component of force F i.e. Fx
BA represents its y-component of force F i.e.,
Therefore, equation (1) can be written as
F= Fx + Fy ----------- (2)
The magnitudes Fx and Fy of the forces Fx and Fy can be found using the trigonometric ratios for the right angled triangle OBA.
In the right angle triangle OBA
\[cos\Theta = \frac{OB}{OA} \]
\[cos\Theta = \frac{F_{x}}{F} \]
Fx = FcosѲ ---------- (3)
In the right angle triangle OBA
\[sin\Theta = \frac{AB}{OA} \]
\[sin\Theta = \frac{F_{y}}{F} \]
Fy = FsinѲ--------- (4)
Equations (3) and (4) give the magnitude of perpendicular components Fx and Fy respectively.
4.6 When a body is said to be in equilibrium?
“A body is said to be in equilibrium if no net force acts on it.”
For example, a book lying on a table is in equilibrium. The weight of the book acting downward is balanced by the upward reaction of the table. As a result, no net force is acting on the book and it is in equilibrium.
4.7 Explain the first condition for equilibrium.
“A body is said to satisfy first condition for equilibrium if the resultant of all the forces acting on it is zero.”
If n number of forces F1, F2, F3 ……. Fn, then first condition of equilibrium can mathematically express as
F1 + F2 + F3 + ……… + Fn = 0
Σ F = 0
4.8 Why there is a need of second condition for equilibrium if a body satisfies first condition for equilibrium.
If a body satisfies first condition for equilibrium the body is still not in equilibrium. It is because the body has the tendency to rotate. This situation demands another condition for equilibrium in addition to the first condition for equilibrium.
4.9 What is second condition for equilibrium?
“A body satisfies second condition for equilibrium when the resultant torque acting
on it is zero. “
Mathematically
Σ τ = 0
4.10 Give an example of a moving body which is in equilibrium.
A paratrooper coming down with terminal velocity is in equilibrium.
4.11 Think of a body which is at rest but not in equilibrium.
A ball thrown upward becomes at the rest at the top. At this state it is not in equilibrium although it is at rest.
4.12 Why a body cannot be in equilibrium due to single force acting on it?
A body cannot be in the state of equilibrium if only a single force acts on it because we need at least two forces equal in magnitude but opposite in direction to cancel out each other. If there is only one force acting, then we can't cancel it out and the net force won't be zero which means the body won't be in state of equilibrium.
4.13 Why the height of vehicles is kept as low as possible?
The height of the vehicles is kept as low as possible to bring its centre of gravity to the lowest position and improve its stability.
4.14 Explain what is meant by stable, unstable, and neutral equilibrium. Give one example in each case?
Stable Equilibrium
Definition
“A body is said to be in stable equilibrium if after a slight tilt it returns to its previous position.”
Example
Consider a book lying on the table. Tilt the book slightly about its one edge by lifting it from the opposite side as shown in the figure below
It returns to its previous position when sets free. Such a state of the body is stable equilibrium.
Position of Centre of Gravity in Stable Equilibrium
When a body is in stable equilibrium, its centre of gravity is at the lowest position. When it is tilted, its centre of gravity rises. It returns to its stable state by lowering its centre of gravity. A body remains in stable equilibrium as long as the centre of gravity acts through the base of the body.
Un-Stable Equilibrium
Definition
“If a body does not return to its previous position when sets free after a slightest tilt is said to be in unstable equilibrium”
Example
Take a pencil and try to keep it in the vertical position on its tip as shown in the figure below
Whenever you leave it, the pencil topples over about its tip and falls down. This is called the unstable equilibrium.
Position of Centre of Gravity in Unstable Equilibrium
The centre of gravity of the body is at its highest position in the state of unstable equilibrium. As the body topples over about its base (tip), its centre of gravity moves towards its lower position and does not return to its previous position.
Neutral Equilibrium
Definition
“If a body remains in its new position when disturbed from its previous position, it is said to be in a state of neutral equilibrium”
Example
Take a ball and place it on a horizontal surface as shown in the figure below.
Roll the ball over the surface and leave it after displacing from its previous position. It
remains in its new position and does not return to its previous position. This is called neutral equilibrium.
Position of Centre of Gravity in Neutral Equilibrium
In neutral equilibrium, the centre of gravity of the body remains at the same height, irrespective to its new position.
FBISE Physics MCQs for Class 9 of Unit 5 Gravitation
5.2 What is meant by the force of gravitation?
Ans: The force due to which everybody of universe attracts every other body is called force of gravitation.
5.3 Do you attract the Earth, or the Earth attracts you? Which one is attracting with a larger force? You or the Earth.
Ans: You attract the earth with the same force that the earth attracts you. However, this force has more effect on you because you are much lighter than Earth.
5.4 What is a field force?
Ans: A force which is acting on a body by another body whether the body is in contact with other body or not, is called field force. It is a noncontact force
Examples:
i. Gravitational Force
ii. Electrostatic force.
iii. Magnetic force
5.5 Why earlier scientists could not guess about the gravitational force?
Ans: Earlier scientists could not guess the force of gravitation between two masses, because it is of very small value. it could be detected only by the very sensitive instrument which was not invented at that time.
5.6 How can you say that gravitational force is a field force?
Ans: The gravitational force exists around earth and it is acting on the bodies whether the bodies are in contact with each other or not, so we can say that gravitational force is a field force.
5.7 Explain, what is meant by gravitational field strength?
Ans: In the gravitational field of the earth, the gravitational force per unit mass is called the gravitational field strength of the earth.
At any place its value is equal to the value of g at that point. Near the surface of the earth, the gravitational field strength is 10 Nkg-1.
5.8 Why law of gravitation is important to us?
Ans: The law of gravitation is important for us because it is used to calculate
i. The Gravitational force of attraction between two masses.
ii. The mass of the earth.
iii. The acceleration due to gravity at any place on the earth.
5.9 Explain the law of gravitation.
Ans: Statement
“Everybody in the universe attracts every other body with a force which is directly proportional to the product of their masses and inversely proportional to the square of the distance between their masses”
Mathematically
\[F = G\frac{m_{1}m_{2}}{d^{2}}\]
5.10 How the mass of Earth can be determined?
Derivation for the Mass of Earth
Consider a body of mass m on the surface of the Earth as shown in figure below
Let the mass of the Earth be Me and radius of the Earth be R. The distance of the body
from the centre of the Earth will also be equal to the radius R of the Earth. According to the law of gravitation, the gravitational force F of the Earth acting on a body is given
by
\[F = G\frac{mM_{e}}{R^{2}}\]
But the force with which Earth attracts a body towards its centre is equal to its weight w. Therefore
F= w = mg ------------------- (2)
By comparing equation (1) and (2)
\[mg = G\frac{mM_{e}}{R^{2}}\]
\[g = G\frac{M_{e}}{R^{2}}\]
\[M_{e}= \frac{R^{2}g}{G}\]
Here
g = gravitational acceleration = 10 ms-2
R = Radius of the earth = 6.4x106 m
G = gravitational constant = 6.67x10-11 Nm2kg-2
Mass M of the Earth can be determined on putting these values in equation (3)
\[M_{e}= \frac{(6,4X10^{6}))^{2}(10))}{6.67X10^{-11}}\]
Me= 6x1024 kg
Thus, mass of the Earth is 6 x 1024 kg.
5.11 Can you determine the mass of our moon? If yes, then what you need to know?
Ans: Yes, we can determine the mass of the moon by the following formula
\[M_{m}= \frac{R^{2}g}{G}\]
Above equation shows that we need to know the following quantities
i. Gravitational acceleration on the surface of the moon i.e. g
ii. Radius of the moon i.e. R.
iii. Gravitational constant G.
5.12 Why does the value of g vary from place to place?
Ans: The value of gravitational acceleration ‘g’ at any place depends upon its distance from the centre of earth. As different places have different distances from the centre of earth there for the value of ‘g’ have different values at these places.
OR
Ans: The value of gravitational acceleration ‘g’ at any place depends upon its distance from the centre of earth. As distance from the centre of earth varies from place to place therefor the value of g varies from place to place.
5.13 Explain how the value of g varies with altitude.
Ans: Altitude is the height of an object or place above sea level. It is denoted by ‘h’. The value of g varies with altitude by the relation
\[g = G\frac{M_{e}}{(R+h)^{2}}\]
This equation shows that value of g decrease with the increase in altitude.
Example
At a height equal to one earth radius above the surface of earth i.e. (h=R), value of g becomes one fourth of its value on the surface of earth.
5.14 What are artificial satellites?
Ans: An object that revolves around a planet is called a satellite. The moon revolves around the Earth so moon isa natural satellite of the Earth.
Scientists have sent many objects into space. Some of these objects revolve around
the Earth. These are called artificial satellites.
5.15 How Newton's law of gravitation helps in understanding the motion of satellites?
Ans A gravitational force of attraction exists between the Earth and the satellite. This force provides the required centripetal force to the satellite to revolve around the Earth. In this way law of gravitation is very important to understand the motion of satellite.
5.16 On what factors the orbital speed of a satellite depends?
Ans: The speed of satellite is given by the relation
\[v_{o} = \sqrt{g_{h}(R+h)}\]
This equation shows that the speed of satellite depends upon the
· The gravitational acceleration i.e., gh
· The distance of the satellite from the centre of earth i.e. (R+h)
5.17 Why communication satellites are stationed at geostationary orbits?
Ans: Communication satellites and weather satellites are often given geostationary orbits, so that the satellite antennas that communicate with them do not have to move to track them but can be pointed permanently at the position in the sky where they stay. A geostationary orbit is a particular type of geosynchronous orbit.
FBISE Physics MCQs for Class 9 of Unit 6 Work and Energy
6.2 Define work. What is its SI unit?
Ans: Definition
“Work is done when a force acting on a body displaces it in the direction of a force”
Work done = Force x displacement
W= FS
SI unit of work is joule (J). It is defined as
“The amount of work is one joule when a force of one newton displaces a body through one meter in the direction of force.”
6.3 When does a force do work? Explain.
Ans: Work is done when a force acting on a body displaces it in the direction of a force.
Work = (Component of force in the direction od displacement)(displacement)
W = Fx S
W = (FcosѲ)S
W = FScosѲ
6.4 Why do we need energy?
Ans: We need energy to do work.
6.5 Define energy, give two types of mechanical energy.
Ans: Energy
“A body possesses energy if it is capable to do work”
There are two types of mechanical energy
1. Kinetic Energy
2. Potential Energy
“The energy possessed by a body due to its motion is called its kinetic energy.”
\[K.E = \frac{1}{2}mv^{2}\]
Potential Energy
“The energy possessed by a body due to its position is known as its potential energy.”
P.E. = mgh
6.6 Define K.E. and derive its relation.
Ans: Definition
“The energy possessed by a body due to its motion is called its kinetic energy.”
Derivation
Consider a body of mass m moving with velocity v. The body stops after moving through some distance S due to some opposing force such as force of friction acting on it. The body possesses kinetic energy and is capable to do work against opposing force F until
all of its kinetic energy is used up.
K.E. of the body = Work done by it due to motion
K.E. = FS ------------------- (1)
As
vi = v
vf = 0
By Newton second law of motion
F= ma
\[a = \frac{F}{m}\]
Since motion is opposed, hence, a is negative.
Using 3rd equation of motion
\[2aS = v_{f}^{2}-v_{i}^{2}\]
Putting values in this equation
\[2(\frac{-F}{m})S = 0-v^{2}\]
\[\frac{2FS}{m} = v^{2}\]
\[ FS = \frac{1}{2}mv^{2} ---- (2)\]
From equation (1) putting FS = K.E in equation (2)
\[ KE = \frac{1}{2}mv^{2}\]
This equation gives the K.E possessed by a body of mass m moving with velocity v.
6.7 Define potential energy and derive its relation.
Ans: Definition
“The energy possessed by a body due to its position is known as its potential energy.”
Derivation
Let a body of mass m be raised up through height h from the ground. The body will acquire potential energy equal to the work done in lifting it to height h. Thus
Potential energy = work done in lifting the body to the height h
P.E. = Fh
Here F = w, force is equal to the weight of the object
P.E. = wh
Here weight of the body = w = mg
P.E. = mgh
This equation gives the Potential Energy possessed by the body with respect to the ground.
6.8 Why fossils fuels are non-renewable form of energy?
Ans: Fossil Fuels are called non-renewable forms of energy because it took millions of years for them to attain the present form. Once they used to get energy and consumed completely, they cannot be renewed or replenished in short duration
6.9 Which form of energy is most preferred and why?
Ans: Solar energy is the most preferred.
Explanation:
Solar energy is the energy coming from the Sun and is used directly and indirectly. Sunlight does not pollute the environment in any way. The sunrays are the ultimate source of life on Earth. If we find a suitable method to use a fraction of the solar energy reaching the Earth, then it would be enough to fulfil our energy requirement.
6.10 How is energy converted from one form to another? Explain.
Ans: Energy cannot be destroyed however it can be converted into some other forms.
Example
1. Rub your hands together quickly. You will feel them warm. You have used your muscular energy in rubbing hands as a result heat is produced. In the process of rubbing hands, mechanical energy is converted into heat energy.
2. Processes in nature are the results of energy changes. For example, some of the heat energy from the Sun is taken up by water in the oceans. This increases the thermal energy. Thermal energy causes water to evaporate from the surface to form water vapours. These vapours rise up and form clouds. As they cool down, they form water drops and fall down as rain. Potential energy changes to kinetic energy as the rain falls. This rainwater may reach a lake or a dam. As the rainwater flows down, its kinetic energy changes into thermal energy while parts of the kinetic energy of flowing water is used to wash away soil particles of rocks known as soil erosion
6.11 Name the five devices that convert electrical energy into mechanical energy.
Ans: Following devices converts electrical energy to mechanical energy.
1. Electric motor
2. Drill machine
3. Electric fan
4. Elevator
5. Electric grinder
6.12 Name a device that converts mechanical energy into electrical energy.
Ans: Electric generator converts mechanical energy into electrical energy.
6.13 What is meant by the efficiency of a system?
Ans: Definition
“Efficiency of a system is the ratio of required form of energy obtained from a system as output to the total energy given to it as input.”
\[Efficiency = \frac{Required form of energy}{total input energy}\]
\[Efficiency = \frac{Required form of energy}{total input energy}X100\]
6.14 How can you find the efficiency of a system?
Ans: We can find efficiency of a system by the following relation6.15 What is meant by the term power?
Ans: Definition
“Power is defined as the rate of doing work.”
Mathematically
\[Power = \frac{Work done}{Time Taken}\]
\[P = \frac{W}{t}\]
Power is a scalar quantity. SI unit of power is watt (W).
6.15 Define watt.
Ans: Definition
“The power of a body is one watt if it does work at the rate of 1 joule per second.”
Mathematically
\[Power = \frac{Work done}{Time Taken}\]
\[P = \frac{W}{t}\]
FBISE Physics MCQs for Class 9 of Unit 7 Properties of Matter
7.1
How kinetic molecular model of matter is helpful in differentiating
various states of matter?
Ans: Kinetic
Molecular Model of Matter
The kinetic molecular model of matter following
important features.
·
Matter is made up of particles called molecules
·
The molecules remain in continuous motion.
·
Molecules attract each other.
Kinetic molecular model is used to explain the three
states of matter - solid, liquid and gas.
Solids
Solids such as a stone, metal spoon, pencil, etc. have
fixed shapes and volume. Their molecules are held close together by strong forces
of attraction. However, they vibrate about their mean positions but do not move
from place to place.
Liquids
The distances between the molecules of a liquid are
more than in solids. Thus, attractive forces between them are weaker.
Like solids, molecules of a liquid also vibrate about their mean position but
are not rigidly held with each other. Due to the weaker attractive
forces, they can slide over one another. Thus, the liquids can flow. The volume
of a certain amount of liquid remains the same but because it can flow hence,
it attains the shape of a container to which it is put.
Gases
Gases such as air have no fixed shape or volume. They
can be filled in any container of any shape. Their molecules have random motion
and move with very high velocities. In gases, molecules are much farther apart
than solids or liquids. Thus, gases are much lighter than solids and liquids.
They can be squeezed into smaller volumes. The
molecules of a gas are constantly striking the walls of a container. Thus, a
gas exerts pressure on the walls of the container.
7.2
Does there exist a fourth state of matter? What is that?
Ans: Yes, there exists a fourth state of
matter called Plasma. It is ionic state of matter in which matter occur in the
form of positive and negative ions.
7.3
What is meant by density? What is its SI unit?
Ans: “Density of a substance is defined as its mass per unit
volume”
Mathematically
![]()
SI unit of density is kilogramme per cubic metre (kgm-3).
7.4
Can we use a hydrometer to measure the density of milk?
Ans: Yes, we can use hydrometer to measure the density of milk.
Explanation
Hydrometer is a
device which is used to measure the density of a liquid. Hydrometers are
calibrated for different uses, such as a lactometer for measuring the density
(creaminess) of milk, a saccharometer for measuring the density of sugar in a
liquid, or an alcoholometer for measuring higher levels of alcohol in spirits
7.5
Define the term pressure.
Ans: “The force acting normally per unit area on the surface of
a body is called pressure”
Mathematically
![]()
![]()
Pressure is a
scalar quantity. In SI units, the unit of pressure is Nm-2 also called pascal (Pa).
Thus
1 Nm-2 = 1 Pa
7.6
Show that atmosphere exerts pressure.
Ans: The fact that atmosphere exerts pressure can be explained
by a simple experiment as given below
Experiment
Take
an empty tin can with a lid. Open its cap and put some water in it. Place it
over flame. Wait till water begins to boil and the steam expels the air out of
the can. Remove it from the flame. Close the can firmly by its cap. Now place
the can under tap water. The can will squeeze due to atmospheric pressure. Why?
When the can is cooled by tap water, the steam in it condenses. As the steam
changes into water, it leaves an empty space behind it. This lowers the
pressure inside the can as compared to the atmospheric pressure outside the
can. This will cause the can to collapse from all directions. This experiment
shows that atmosphere exerts pressure in all directions.
7.7
It is easy to remove air from a balloon, but it is very difficult
to remove air from a glass bottle. Why?
Ans: This is because the pressure of air inside the balloon is
comparatively high than the atmospheric
pressure outside but pressure of air in glass bottle is equal to the
atmospheric pressure outside. That is why it is difficult to remove air from
glass bottle.
7.8
What is a barometer?
Ans: “The
instruments that measure atmospheric pressure are called barometers”
Mercury barometer
One of the
simple barometers is a mercury barometer. It consists of a glass tube 1m long
closed at one end. After filling it with mercury, it is inverted in a mercury
trough. Mercury in the tube descends and stops at a certain height. The column
of mercury held in the tube exerts pressure at its base. At sea level the
height of mercury column above the mercury in the trough is found to be about
76 cm. Pressure exerted by 76 cm of mercury column is nearly 101,300 Nm equal
to atmospheric pressure. It is common to express atmospheric pressure in terms
of the height of mercury column. As the atmospheric pressure at a place does
not remains constant, hence, the height of mercury column also varies with atmospheric
pressure.
7.9
Why water is not suitable to be used in a barometer?
Ans: Mercury is 13.6 times denser than water. Atmospheric
pressure can hold vertical column of water about 13.6 times the height of
mercury column at a place. Thus, at sea level, vertical height of water column
would be 0.76 m x 13.6 = 10.34 m. Thus, a glass tube
more than 10 m long is required to make a water barometer which becomes
inconvenient. Therefore, use of water in the construction of barometer is not
suitable
7.10
What makes a sucker pressed on a smooth wall sticks to it?

Ans: The sucker is dish-shaped, when pressed against a smooth
surface the air is forced beneath the sucker. The rubber makes an airtight seal
and the air pressure outside is greater than the air pressure beneath the
sucker, thus forcing rubber sucker to ‘stick’
7.11
Why does the atmospheric pressure vary with height?
Ans: Air is a mixture of gases. The
density of air in the atmosphere is not uniform. It decreases continuously as we
go up. The air become thinner and thinner as we go up. Hence the atmospheric
pressure decreases as we go up.
Atmospheric pressure reduce with altitude for two reasons-both
related to gravity.
The gravitation attraction (g) between the earth and air molecule
is greater for those molecules nearer to earth than those further away – they
have more weight – dragging them close together and increasing the pressure
(force per unit area) between them.
Molecules further away from the earth have less weight (because
gravitational attraction is less) but they are also ‘standing’ on the molecules
below them, causing compression. The lower down have to support more molecules
above them and are further compressed (pressurized) in the process.
Note: It is gravitational
force minus the effect of the Earth’s spin (an effect that is greatest at the
equator)
7.12
What does it mean when the atmospheric pressure at a place fall
suddenly?
Ans: A sudden fall in atmospheric pressure
often followed by a storm, rain and typhoon to occur in few hours time.
7.13
What changes are expected in weather if the barometer reading shows
a sudden increase?
Ans: A rapid
increase in atmospheric pressure means that it will soon be followed by a
decrease in the atmospheric pressure indicating poor weather ahead.
7.14
State Pascal's law.
Ans: Pascal's law
“Pressure, applied at any point of a liquid enclosed in a
container, is transmitted without loss to all other parts of the liquid.”
7.15
Explain the working of hydraulic press.
Ans: Hydraulic Press
Hydraulic press is a machine which works on Pascal's
law. It consists of two cylinders of different cross-sectional areas as shown
in figure

They
are fitted with pistons of cross-sectional areas ‘a’ and ‘A’. The object to be
compressed is placed over the piston of large cross-sectional area A. The force
F2 is applied on the piston of small cross-sectional area a. The
pressure P produced by small piston is transmitted equally to the large piston
and a force F2 acts on A which is much larger than F1
Pressure
on piston of small area ‘a’ is given by
![]()
Apply
Pascal's law, the pressure on large piston of area A will be the same as on
small piston.
![]()
Comparing
the above equations, we get
![]()
![]()
![]()
Since
the ratio ![]() is greater than 1, hence the force F2
that acts on the larger piston is greater than the force F1 acting
on the smaller piston.
is greater than 1, hence the force F2
that acts on the larger piston is greater than the force F1 acting
on the smaller piston.
Hydraulic
systems working in this way are known as force multipliers.
7.16
What is meant by elasticity?
Ans: “The
property of a body to restore its original size and shape as the deforming
force ceases to act is called elasticity.”
7.17
State Archimedes principle.
Ans: Archimedes Principle
“When an object is totally or partially immersed in a
liquid, an upthrust act on it equal to the weight of the liquid it displaces”
7.18
What is upthrust? Explain the principle of floatation.
Ans: Upthrust
“When an object
is kept inside a liquid an upward force acts on the object. This upward force
is called the upthrust of the liquid.”
Principle of
Floatation
Statement
“A floating object displaces a fluid having weight equal
to the weight of the object”
Explanation
An object sinks if its weight is greater than the upthrust
acting on it. An object floats if its weight is equal or less than the
upthrust. When an object floats in a fluid, the upthrust acting on it is equal
to the weight of the object. In case of floating object, the object may be partially
immersed. The upthrust is always equal to the weight of the fluid displaced by
the object. This is the principle of floatation.
7.19
Explain how a submarine moves up the water surface and down into
water.
Ans: A submarine can travel over as well
as under water. It works on the principle of floatation. It floats over water
when the weight of water equal to its volume is greater than its weight. Under
this condition, it is similar to a ship and remains partially above water
level. It has a system of tanks which can be filled with and emptied from seawater.
When these tanks are filled with seawater, the weight of the submarine
increases. As soon as its weight becomes greater than the upthrust, it dives
into water and remains under water. To come up on the surface, the tanks are
emp tied from seawater.
7.20
Why does a piece of stone sink in water but a ship with a huge weight
float?
Ans: It is due to Archimedes principle. The density of ship is
less, it displaces more liquid, experience more upward thrust and floats
whereas the density of stone is more, it displaces less liquid experience less
upward thrust and sinks.
The stone sinks
because the upthrust force acting on the stone is smaller than its weight. The
ship of huge weight floats on the surface of water because it is designed in
such a way that its volume is so large, so the upthrust force balances the
weight of the ship.
As the weight
of stone is greater the weight of liquid it displaces so that’s why stone sinks in water but weight of ship is less or equal to
the weight of the liquid it displaces that’s why ship floats.
7.21
What is Hooke's law? What is meant by elastic limit?
Ans: Hooke's
law
“The strain produced in a body by the stress applied to it
is directly proportional to the stress within the elastic limit of the body.”
Mathematically
Stress ∝ strain
stress = constant X strain
![]()
Elastic Limit
“The maximum stress
that can be safely applied on a body without causing permanent deformation in
its length, volume or shape is called its elastic limit”
7.22
Take a rubber band. Construct a balance of your own using a rubber
band. Check its accuracy by weighing various objects.
Ans: It is activity exercise not
important for FBISE Physics examination point of view.
FBISE Physics MCQs for Class 9 of Unit 8 Thermal Properties of Matter
8.1
Why does heat flow from hot body to cold body?
The atoms in the hot bodies have higher kinetic
energy than those of the cold bodies. Thus, to maintain thermal
equilibrium, the atoms of higher kinetic energy tries to move and collide
with the atoms of low kinetic energy. Thus, heat transfers from a hot
body to a cold body.
8.2
Define the terms heat and temperature.
“Heat is the
energy that is transferred from one body to the other in thermal contact with
each other as a result of the difference of temperature between them.”
Temperature:
“Temperature of a body is the degree of hotness or
coldness of the body”
8.3
What is meant by internal energy of a body?
Internal Energy
“The sum of kinetic energy and
potential energy associated with the atoms, molecules and particles of a body
is called its internal energy.”
8.4
How does heating affect the motion of molecules of a gas?
When a gas is heated its temperature increase, as the temperature
is the measure of average kinetic energy of gas molecules, therefore motion of
gas molecules also increases.
8.5
What is a thermometer? Why mercury is preferred as a thermometric
substance?
Thermometer
“A device that is used to measure the temperature of
a body is called thermometer”
Why mercury is preferred as a thermometric substance
Mercury freezes at -39 °C and boils at 357 °C. It has all the
thermometric properties. Thus, mercury is one of the most suitable thermometric
material. Mercury-in-glass thermometers are widely used in laboratories,
clinics and houses to measure temperatures in the range from -10 °C to 150 °C.
8.6
Explain the volumetric thermal expansion.
Volume Thermal Expansion
“The volume of a solid changes with the change in temperature and
is called volume thermal expansion or cubical thermal expansion.”
Explanation
Consider a solid of initial volume Vo at certain
temperature To . On
heating the solid to a temperature T, let its volume becomes V,
then
Change in the volume of a solid = 𝛥V = V - Vo
Change in temperature = 𝛥T = T - To
The change in volume 𝛥V is
proportional to its original volume Vo and
change in temperature 𝛥T.
Thus
𝛥V ∝ Vo 𝛥T
𝛥V =βVo 𝛥T --------- (1)
V - Vo
= βVo 𝛥T
V = Vo +
βVo 𝛥T
V = Vo (1+β 𝛥T) -------- (2)
Where β is the temperature coefficient of volume expansion. Using
equation (1) we get
![]()
Thus, we can define the temperature coefficient of volume expansion
β as
“The fractional change in volume per kelvin change in temperature.”
8.7
Define specific heat. How would you find the specific heat of a
solid?
“Specific heat
of a substance is the amount of heat required to raise the temperature of 1 kg
mass of that substance through 1K.”
Mathematically
![]()
Explanation
Generally, when
a body is heated, its temperature increases. Increase in the temperature of a
body is found to be proportional to the amount of heat
absorbed by it.
It has also been observed that the quantity of heat 𝛥Q required to
raise the temperature 𝛥T of a body is
proportional to the mass m of the body.
Thus
𝛥Q ∝ m𝛥T
𝛥Q = c m𝛥T
Here 𝛥Q is the amount
of heat absorbed by the body and c is the constant of proportionality called
the specific heat capacity or simply specific heat and is given by the relation
![]()
In SI units,
mass m is measured in kilogramme (kg), heat 𝛥Q is measured in joule (J) and temperature increase 𝛥T is taken in kelvin (K). Hence, SI unit of
specific heat
is Jkg-1K-1.
8.8
Define and explain latent heat of fusion.
“Heat energy required to change unit
mass of a substance from solid to liquid state at its melting point without
change in its temperature is called its latent heat of fusion”
Latent heat of Fusion is denoted by Hf and
mathematically given by the relation
![]()
Explanation
Generally, when a body is heated, its temperature increases.
Increase in the temperature of a body is found to be proportional to the amount
of heat
absorbed by it. It has also been observed that the quantity of heat
𝛥Q required to raise the temperature 𝛥T of a body is proportional to the mass m of the body.
Thus
𝛥Q ∝ m𝛥T
𝛥Q = c m𝛥T
Here 𝛥Q is the amount
of heat absorbed by the body and c is the constant of proportionality called
the specific heat capacity or simply specific heat and is given by the relation
![]()
In SI units, mass m is measured in kilogramme (kg), heat 𝛥Q is measured in joule (J) and temperature increase 𝛥T is taken in kelvin (K). Hence, SI unit of
specific heat is Jkg-1K-1.
8.9
Define latent heat of vaporization.
Definition
“The quantity of heat that changes unit mass of a liquid completely
into gas at its boiling point without any change in its temperature is called
its latent heat of vaporization.”
Latent heat of Fusion is denoted by Hv and
mathematically given by the relation
![]()
8.10
What is meant by evaporation? On what factors the evaporation of a
liquid depends. Explain how cooling is produced by evaporation.
Definition
“Evaporation is the changing of a liquid into vapours
(gaseous state) from the surface of the liquid without heating it.”
Factors on which Evaporation of a Liquid Depends
Evaporation takes place at all temperature from the surface of a
liquid. The rate of evaporation depends upon following factors
i.
Temperature
At higher temperature, more molecules of a liquid are moving with
high velocities. Thus, more molecules escape from its surface. Thus,
evaporation is faster at high temperature than at low temperature.
ii.
Surface
Area
Larger is the surface area of a liquid, greater number of molecules
has the chance to escape from its surface.
iii.
Wind
Wind blowing over the surface of a liquid sweeps away the liquid
molecules that have just escaped out. This increases the chance for more liquid
molecules to escape out.
iv.
Nature
of the Liquid
Liquids differ in the rate at which they evaporate.
Cooling is Produced by Evaporation
During evaporation fast moving molecules escape out
from the surface of the liquid. Molecules that have lower kinetic energies are
left behind. This lowers the average kinetic energy of the liquid molecules and
the temperature of the liquid. As a result, cooling is produced.
FBISE Physics MCQs for Class 9 of Unit 9 Transfer of Heat
FBISE Physics MCQs for Class 10
FBISE Physics MCQs for Class 10 of Unit 10 Simple Harmonic Motion and Waves
10.1
What is simple harmonic motion? What are the
necessary conditions for a body to
execute simple harmonic motion?
Ans: “Simple
harmonic motion occurs when the net force is directly proportional to the
displacement from the mean position
and is always directed towards the mean position.”
Conditions for a body to execute Simple Harmonic Motion (SHM)
i
A
body executing SHM always vibrates about a fixed position.
ii
Its
acceleration is always directed towards the mean position.
iii
The
magnitude of acceleration is always directly proportional to its displacement
from the mean position.
10.2
Think of several examples of motion in everyday life
that are simple harmonic.
Ans: Examples of SHM in everyday life
i
Vibratory motion of pendulum of a clock.
ii Vibratory motion of a swing
iii Vibratory motion of a cradle
iv Vibratory motion of
human ear drums
v Vibratory motion of strings of a guitar.
10.3 What are damped
oscillations. How damping progressively reduces the amplitude
of oscillation?
Ans: “The
oscillations of a system in the presence of some resistive force are damped oscillations”
Damping reduces the amplitude of the oscillations
The force of friction retards the
motion, so the systems do not oscillate indefinitely. The
friction reduces the mechanical energy of the system as time passes, and the
motion is said to be damped. This damping progressively reduces the amplitude of the vibration of motion as shown in the figure below

10.4 How can you define the
term wave? Elaborate the difference between mechanical
and electromagnetic waves. Give examples of each.
Ans: “A wave is a disturbance in the medium which causes the particles of the medium to undergo vibratory motion about their mean position in equal intervals of time.”
Damping reduces the amplitude of the oscillations
|
Mechanical
waves |
Electromagnetic
Waves |
|
|
1 |
Waves which require any medium for their propagation are
called mechanical waves. Examples water waves, sound |
Waves which do not require any Examples Radio waves, television waves, X-rays, heat and light
waves |
|
2 |
Mechanical waves cannot travel
through vacuum. |
Electromagnetic
waves can travel through vacuum. |
|
4 |
Mechanical waves are produced due
to the vibrations of the particle of the medium. |
Electromagnetic waves are produced
by the vibration of the charged particles OR 1. Electromagnetic waves are
formed due to the oscillating electrical and magnetic field. |
|
5 |
Mechanical waves have speed much
lessor than speed of light. |
Electromagnetic
waves travel at the speed of light. |
10.5 Distinguish between
longitudinal and transverse waves with suitable examples.
|
Sr. No. |
Longitudinal Waves |
Transverse Waves |
|
1 |
In longitudinal waves the vibratory motion of
the particles of the medium is parallel to the direction of propagation of
wave. Example Sound
waves. seismic P-waves,
Ultrasound. |
In transverse waves, the vibratory motion of
particles of the medium is perpendicular to the direction of propagation of
waves. Example Waves on the surface of water, light waves, seismic S waves |
|
2 |
Longitudinal waves consist of rarefactions
and compressions. |
Transverse
waves consist of crests and troughs. |
|
4 |
Longitudinal waves act in one dimension |
Transverse
Waves acts in two dimensions. |
|
5 |
Longitudinal wave cannot be polarized. |
Transverse wave can be polarized. |
|
6 |
Transverse waves can be produced in any
medium such as gas, liquid or solid. |
Longitudinal waves can be produced in solid
and liquid’s surface. |
10.6 Draw a transverse wave
with an amplitude of 2 cm and a wavelength of 4 cm. Label a
crest and trough on the wave.

10.7 Derive a relationship
between velocity, frequency, and wavelength of a wave. Write a
formula relating of a wave to its time period and wavelength. Velocity
Ans: Wave is a
disturbance in a medium which travels from one place to another and hence has a
specific velocity of travelling. This is called the velocity of wave.
Velocity of
wave is defined by
![]()
![]() -------- (1)
-------- (1)
If time taken by the wave in moving from one
point to another is equal to its time period T, i.e., t=T then the distance
covered by the wave will be equal to one wavelength ʎ i.e., d=ʎ
Putting t=T and d=ʎ in equation in (1)
![]()
![]() ------- (2)
------- (2)
As the frequency is the reciprocal of time
period i.e. ![]()
Putting ![]() in equation (2)
in equation (2)
v = ʎ f
This is the required relation between velocity,
frequency, and wavelength of the wave.
10.8 Waves are the means of
energy transfer without transfer of matter. Justify this
statement with the help of a simple experiment.
waves transfer energy
from one place to another without transfer of matter. This is explained in the
simple experiment given below
Experiment
Drop a stone into a
pond of water. Water waves will
be produced on the surface of water and will travel outwards as shown in the figure below
Place a cork at some
distance from the falling
stone. When waves reach the cork, it will move up and down along with the motion of the water particles by
getting energy from the waves.
This activity shows
that waves transfer energy
from one place to another without transferring matter, i.e., water.
10.9 Explain the following
properties of waves with reference to ripple tank experiment:
a. Reflection
b. Refraction
c. Diffraction
Ans:
Reflection of wave
Definition
“When
waves moving in one medium fall on the surface of another medium, they bounce back into the first
medium such that
the angle of incidence is equal to the angle of reflection.”
Reflection
of wave with reference to ripple tank
Place a barrier
in the ripple tank. The water waves will reflect from the
barrier . If the barrier is placed at an angle to the wavefront, the reflected
waves can be seen to obey the law of reflection i.e., the
angle of the incident wave along the normal will be equal to
the angle of the reflected wave as shown in the figure below


Refraction of wave
Definition
“When
a wave from one medium enters into the second medium at some angle, its direction of travel changes.”
Refraction of wave with reference to ripple tank
If a block is submerged in the ripple tank, the depth of water in the tank will be shallower over the block than elsewhere. For
the observation of refraction of water waves submerge the block in the ripple
tank such
that the boundary between the deep and the
shallower water is at some angle to the wavefront Now,
we will observe that the waves change their direction of
propagation as shown I n the figure below.

Note that the direction of
propagation is always normal to the wavefronts. This change
of path of water waves while passing from a region of
deep water to that of shallower one is called refraction.
Diffraction of wave
Definition
“The
bending or spreading of waves around the sharp edges or corners of obstacles or slits is called diffraction.”
Diffraction of wave with reference to ripple tank
To observe the phenomenon of diffraction of water waves. Generate straight waves in a ripple tank and place two obstacles
in line in such a way that separation between them is equal to the wavelength of water waves. After passing through a small slit between the two obstacles, the waves will spread in every direction and change into almost semi-circular pattern as shown
in the figure below

Diffraction of water waves through
small slit
10.10 Does increasing the
frequency of a wave also increase its wavelength? If not, how
are these quantities related?
Ans: No, if we increase the frequency of
a wave its wavelength decreases provided that the medium through which wave is
passing remain the same.
The wavelength and frequency of a wave are related by the relation
v = fʎ
ʎ = ![]()
As the velocity of the wave will be fixed by
the medium through which wave is travelling, therefore
ʎ = ![]()
i.e., wavelength and frequency are inversely
proportional to each other.
.











Comments
Post a Comment