Physics Class 9 Chapter 4 (Exercise Solution)
UNIT No. 4
Turning Effect of Forces
Exercise
i.
Two equals but unlike parallel forces having different line of
action produce
(a) a torque (b) a
couple
(c) equilibrium (d) neutral
equilibrium
ii.
The number of forces that can be added by head to tail rule are:
(a) 2 (b) 3 (c)
4 (d)
any number
iii.
The number of perpendicular components of a force are:
(a) 1 (b) 2 (c)
3 (d)
4
iv.
A force of 10 N is making an angle of 30° with the horizontal. Its
horizontal component will be:
(a) 4 N (b)
5 N (c) 7 N (d) 8.7 N
v.
A couple is formed by
(a) two forces
perpendicular to each other
(b) two like
parallel forces
(c) two equal
and opposite forces in the same line
(d) two equal
and opposite forces not in the same line
vi.
A body is in equilibrium when its:
(a) acceleration
is uniform
(b) speed is
uniform
(c) speed and
acceleration are uniform
(d)
acceleration is zero
vii.
A body is in neutral equilibrium when its centre of gravity:
(a) is at its
highest position
(b) is at the
lowest position
(c) keeps its
height if displaced
(d) is situated
at its bottom
viii.
Racing cars are made stable by:
(a) increasing
their speed
(b) decreasing
their mass
(c) lowering
their centre of gravity
(d) decreasing
their width
Answers to
Multiple Choice Questions (MCQs)
|
i.
|
(b) |
ii.
|
(d) |
|
iii.
|
(b) |
iv.
|
(d) |
|
v.
|
(d) |
vi.
|
(d) |
|
vii.
|
(c) |
viii.
|
(c) |
4.2
Define the following:
(i) resultant vector
(ii) torque
(iii) centre of mass
(iv) center of gravity
Ans: Resultant
Vector
“A
resultant vector is a single vector that has the same effect as the combined
effect of all the vectors to be added.”
Torque
“The
turning effect of a force is called torque or moment of the force.”
Torque
is denoted by the symbol τ and is given by the relation
τ = F x L
Torque
is a vector quantity, and its SI unit is newton-meter (Nm).
Centre
of Mass
“Centre
of mass of a system is such a point where an applied force causes the system to
move without rotation”
Generally,
centre of mass of a system is represented by “O”.
Centre
of gravity
“A
point where the whole weight of the body appears to act vertically downward is
called centre of gravity of a body”
Generally,
centre of gravity of a body is represented by “G”.
4.3
Differentiate the following:
(i) like and unlike forces
(ii) torque and couple
(iii) stable and neutral equilibrium
Ans:
(i)
Like and Unlike Forces
|
Sr. # |
Like Parallel forces |
Unlike Parallel Forces |
|
1 |
Like parallel forces are the forces that are
parallel to each other and have the same direction. |
Unlike parallel forces are the forces that are
parallel but have directions opposite to each other |
(ii)
Torque and Couple
|
Sr. # |
Torque |
Couple |
|
1. |
The
turning effect of the force is called torque. |
A
couple is formed by two unlike parallel forces of same magnitude but not
acting along the same line. |
|
2. |
Torque
is produced by a single force. |
Couple
is formed by two forces. |
|
3. |
Torque
is the product of force and moment arm L. Torque=
Force x Moment arm |
Torque
Produced by the couple is given by the product of one of the two forces and
the perpendicular distance between them. |
|
4. |
Examples
i.
Unscrewing a nut using a wrench.
ii.
Open or closing a door by pushing it about its hinges. |
Examples
i.
Turning a steering wheel of a car by applying two hands
form a couple.
ii.
Turning
of a tap is based upon the principle of couple. |
|
5. |
In the case of a FREE
body (not fixed to a pivot), a torque produces not only rotational motion but
also translational motion of the body. |
A couple NEVER
produces translational motion in a free body. |
(iii) Stable and Neutral
Equilibrium
|
Sr.# |
Stable Equilibrium |
Neutral Equilibrium |
|
1 |
A
body is said to be in stable equilibrium if after a slight tilt it returns to
its previous position |
If
a body remains in its new position when disturbed
from its previous position, it is said to be in a state of neutral
equilibrium. |
|
2 |
When a body is in stable equilibrium, its centre of gravity is at
the lowest position. |
In neutral equilibrium, the centre of gravity of the body
remains at the same height, irrespective to its new |
|
3 |
A
body remains in stable equilibrium as long as the centre of gravity acts
through the base of the body |
In
neutral equilibrium, all the new states in which a body is moved, are the
stable states and the body, remains in its new state |
|
4 |
Examples
of stable equilibrium ·
Chair lying
on the floor ·
The heavy
base of the vehicle ·
Table lying
on the ground ·
Cone lying on
its base by lowering its centre of gravity ·
Bottle lying
on its base |
Examples
of neutral equilibrium ·
Ball moving
on the ground ·
Motion of
sphere ·
A roller ·
A pencil
lying horizontally ·
An egg lying
horizontally on a flat surface |
4.4
How head to tail rule helps to find the
resultant of forces?
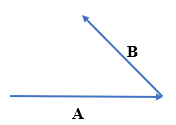
First select a suitable scale. Then draw the vectors of all the
forces according to the scale, such as vectors A and B as shown in the figure
blow
Take any one of the vectors as first vector e.g., vector A. Then
draw next vector B such that its tail coincides with the head of the first
vector A. as shown in the figure below.
Similarly, draw the next vector for
the third force (if any) with its tail coinciding with the head of the previous
vector and so on.
Now draw a vector R such that its tail is at the tail of vector A,
the first vector, while its head is at the head of vector B, the last vector as
shown in figure below.
Vector R represents the resultant force completely in magnitude and
direction.
4.5
How can a force be resolved into its perpendicular components?
Resolution of Forces
Definition
“Splitting up of a force into two mutually perpendicular
components is called the resolution of that force”
Method of Resolving a Force into its perpendicular components
Consider a force F represented by line OA
making an angle q with x-axis as shown in the figure below
Draw a perpendicular AB on x-axis from A.
According to head to tail rule, OA is the resultant of vectors represented
by OB and BA. Thus
OA = OB + BA -------- (1)
The components OB and BA are
perpendicular to each other. They are called the perpendicular components of OA
representing force F.
Here
OB represents x-component of force F i.e. Fx
BA represents
its y-component of force F i.e.,
Therefore, equation (1) can be written as
F=
Fx + Fy
----------- (2)
The magnitudes Fx and Fy of the forces Fx and Fy can
be found using the trigonometric ratios for the right angled triangle OBA.
In the right angle triangle OBA
\[cos\Theta = \frac{OB}{OA} \]
\[cos\Theta = \frac{F_{x}}{F} \]
Fx = FcosѲ ---------- (3)
In the right angle triangle OBA
\[sin\Theta = \frac{F_{y}}{F} \]
Fy = FsinѲ--------- (4)
Equations (3) and (4) give the magnitude of perpendicular
components Fx and Fy respectively.
4.6
When a body is said to be in equilibrium?
“A body is
said to be in equilibrium if no net force acts on it.”
For
example, a book lying on a table is in equilibrium. The weight of the
book acting downward is balanced by the upward reaction of the table. As a result,
no net force is acting on the book and it is in equilibrium.
4.7
Explain the first condition for equilibrium.
“A body is said to satisfy first condition for equilibrium
if the resultant of all the forces acting on it is zero.”
If n number of forces F1, F2, F3
……. Fn, then first condition of equilibrium can mathematically express
as
F1
+ F2 + F3 + ……… + Fn = 0
Σ
F = 0
4.8
Why there is a need of second condition for
equilibrium if a body satisfies first condition for equilibrium.
If a body satisfies first condition for equilibrium the
body is still not in equilibrium. It is because the body has the tendency to rotate.
This situation demands another condition for equilibrium in addition to the
first condition for equilibrium.
4.9
What is second condition for equilibrium?
“A body satisfies second condition for equilibrium
when the resultant torque acting
on it is zero. “
Mathematically
Σ
τ = 0
4.10 Give an example of a
moving body which is in equilibrium.
A paratrooper coming down with terminal velocity is
in equilibrium.
4.11 Think of a body which
is at rest but not in equilibrium.
A ball thrown upward becomes at the rest at the top. At
this state it is not in equilibrium although it is at rest.
4.12 Why a body cannot be
in equilibrium due to single force acting on it?
A body cannot be in the state of
equilibrium if only a single force acts on it because we need at least two forces
equal in magnitude but opposite in direction to cancel out each other. If there
is only one force acting, then we can't cancel it out and the net force won't
be zero which means the body won't be in state of equilibrium.
4.13 Why the height of
vehicles is kept as low as possible?
The height of the vehicles is kept as low as
possible to bring its centre of gravity to the lowest position and improve its stability.
4.14 Explain what is meant
by stable, unstable, and neutral equilibrium. Give one example in each case?
Stable Equilibrium
Definition
“A body is said to be in stable equilibrium if after
a slight tilt it returns to its previous position.”
Example
Consider a book lying on the table. Tilt the book slightly about its one edge by lifting it from the opposite side as shown in the figure below
It returns to its previous position when sets free.
Such a state of the body is stable equilibrium.
Position of Centre of Gravity in Stable Equilibrium
When a body is in stable equilibrium, its centre of gravity is at the lowest position. When it is tilted, its centre of gravity rises. It returns to its stable state by lowering its centre of gravity. A body remains in stable equilibrium as long as the centre of gravity acts through the base of the body.
Un-Stable Equilibrium
Definition
“If a body does not return to its previous position when
sets free after a slightest tilt is said to be in unstable equilibrium”
Example
Take a pencil and try to keep it in the vertical position on its
tip as shown in the figure below
Whenever you leave it, the pencil topples over about its tip and
falls down. This is called the unstable
equilibrium.
Position of Centre of Gravity in Unstable Equilibrium
The centre of gravity of the body is at its highest position in the state of unstable equilibrium. As the body topples over about its base (tip), its centre of gravity moves towards its lower position and does not return to its previous position.
Neutral Equilibrium
Definition
“If a body remains in its new position when disturbed
from its previous position, it is said to be in a state of neutral equilibrium”
Example
Take a ball and place it on a horizontal surface as shown in the
figure below.
Roll the ball over the surface and leave it after
displacing from its previous position. It
remains in its new position and does not return to its previous position. This
is called neutral equilibrium.
Position of Centre of Gravity in Neutral Equilibrium
In neutral equilibrium, the centre of gravity of the body
remains at the same height, irrespective to its new position.










Comments
Post a Comment